| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- Skip Connection
- cnn
- GCN
- Optimizer
- RNN
- Bottleneck Layer
- Inception Module
- Manager
- DCGAN
- vim-plug
- DL
- Inception V1
- jupyter
- AI
- Vanilla RNN
- Residual Connection
- ResNet
- Generative
- Peephole Connection
- version
- virtualenv
- iTerm2
- python
- Skip Connectioin
- sigmoid
- Gated Skip Connection
- Linear
- GoogLeNet
- Regression
- classification
- Today
- Total
IT Repository
(2) What is Gradient Descent? (Optimization) 본문
How to minimize cost¶
(손실을 나타내는 loss와 cost는 서로 동일한 의미로 사용됩니다.)
아래부터는 조금 수식이 복잡해 질 수 있으므로 편의상 b=0인 경우로 수식을 간략화하겠습니다.
$H(x) = wx \\ cost(w) = \dfrac{1}{m} \displaystyle \sum_{i=1}^{m} \big( wx^{(i)} - y^{(i)} \big)^2$
그러면 이제 모델이 얼마나 좋은지 나쁜지에 대해서는 계산할 수 있는데, 어떻게 가장 좋은 모델을 찾아낼 수 있을까요?
우선 가능한 w에 대해서 모두 대입해보는 것이 가능할 것입니다.
이와 같이 파라미터(w)가 1개인 경우에는 가능할 수도 있지만, 파라미터가 20만개 이상되는 일반적인 DL 모델에서는 거의 불가능할 것입니다.
따라서, 우리는 이와 같이 생각해보려고 합니다.
- Cost function은 w값에 대한 cost가 반환되는 함수이다.
- 따라서 Cost function의 값이 가장 낮아지는 부분을 찾는다면, 그 때의 w값이 최적의 값이다.
- 함수의 최소값에서는 기울기가 0, 즉 미분값이 0이다.
Gradient Descent¶
(아래 그래프를 참고하면 좀더 이해가 쉽습니다.)
현재의 w와 cost가 그래프 상의 어느 지점이라고 할 때, 경사가 낮아지는 쪽으로 계속 움직이면 결국에는 경사가 0인 지점을 찾을 것입니다.
즉, Loss function의 도함수를 통해 미분값이 0이 되는 지점을 찾아내려가는 것이 Gradient Descent 알고리즘의 개념입니다. (Gradient는 경사도, 즉 미분값을 의미합니다.)
$Loss'(w) = \dfrac{\delta~Loss}{\delta~w} (= \text{Gradient})$
import numpy as np
import matplotlib.pyplot as plt
min_cost = 10
w = np.linspace(-3, 5, 801)
cost = 5*(w-1)**2 + min_cost
plt.title("Graph of Cost(w)")
plt.plot(w, cost)
plt.plot(np.arange(-4, 6), np.full(10, min_cost), "r", label="Lowest cost")
plt.scatter([4, -1], [55, 30], s=50, c="Green")
plt.quiver(3.8, 54, -1-3.6, 30-53, scale_units='xy', angles='xy', scale=1, width=0.005)
plt.annotate("w updated from 4 to -1",
xy=[1.5, 45], xytext=[0, 60],
arrowprops={'facecolor':'0.0', 'arrowstyle':'->'})
plt.xlim([-3, 5]); plt.ylim([0, 100])
plt.yticks(np.arange(0, 101, 10))
plt.xlabel("w"); plt.ylabel("cost")
plt.legend()
plt.show()
Gradient Descent의 수치해석적 이해¶
그러면 한번 Gradient Descent 알고리즘을 한 스텝 따라가 봅시다.
여기에서는 미분을 계산하지는 않고, 기울기와 미분값의 개념만을 이해합니다.
(1)
우선, $w = 4$ 인 지점에서의 Gradient가 5 라고 가정해봅시다.
Gradient가 양수값입니다.
따라서 그래프상으로 오른쪽으로 움직이면 Loss는 증가할 것입니다.
반대로 왼쪽으로 움직이면 Loss가 감소할 것입니다.
(위 그래프의 2, 3, 4 구간)
(2)
w를 왼쪽으로 움직이기 위해 Gradient의 크기만큼 빼줍니다.
이를 통해서 우리는 Gradient가 크다면 많이 움직이고, 작다면 조금 움직이게 할 수 있습니다.
$\begin{eqnarray} w^\ast &=& w - \text{Gradient} \\ &=& 4 - 5 \\ &=& -1 \end{eqnarray}$
w가 w*로 업데이트 되었습니다.
그런데 문제는 w가 4에서 -1로 너무 많이 움직였다는 것입니다.
위의 그래프를 참고하면, 심지어 이미 최소값을 지나버렸습니다.
(3)
따라서 learning rate라는 상수값($\alpha$)을 곱해서, Gradient의 크기에 정비례하되 너무 크지 않게 움직이도록 합니다.
(여기서 $\alpha = 0.001$로 가정합니다.)
$\begin{eqnarray} w^\ast &=& W - \alpha \cdot \text{Gradient} \\ &=& 4 - 0.005 \\ &=& 3.995\\ \end{eqnarray}$
이제 w가 손실값을 줄이도록 적절히 업데이트 되었습니다.
이를 반복하면 결국 미분값이 0이 되는 지점, 손실값이 가장 작아지는 지점을 찾아갈 것입니다.
Gradient Descent의 수식적 이해¶
위와 같이 수치해석적으로 대입할 수도 있지만 매번 똑같은 과정의 계산을 해야 합니다.
기울기에 대한 계산인 이상 도함수에 대입하는 것이 수학적으로 좀더 올바른 접근일 것입니다.
따라서 이번에는 Loss function을 편미분하여 그 도함수를 사용해보겠습니다.
$L(w) = \dfrac{1}{m} \displaystyle \sum_{i=1}^{m} \big( wx^{(i)} - y^{(i)} \big)^2$
(1)
미분을 하면, 지수에 있는 2가 상수로 내려올 것이므로 수식상의 간결함을 위해 분모에 미리 2를 곱합니다.
(m 자체도 이미 상수이므로 곱해도 결과는 같습니다.)
$L(w) = \dfrac{1}{2m} \displaystyle \sum_{i=1}^{m} \big( wx^{(i)} - y^{(i)} \big)^2$
(2)
위에서 해보았듯이 파라미터 w가 업데이트되는 수식(Optimizer)은 아래와 같습니다.
$w := w - \alpha \cdot \dfrac{\delta}{\delta~W} L(w)$
(3)
이제 수식을 정리합니다.
$\begin{eqnarray} w &:=& w - \alpha \cdot \dfrac{\delta}{\delta~w} L(w) \\ &:=& w - \alpha \cdot \dfrac{\delta}{\delta~w} \left( \dfrac{1}{2m} \displaystyle \sum_{i=1}^{m} \big( wx^{(i)} - y^{(i)} \big)^2 \right) & ~~~~~~~~~~ \text{손실함수를 대입합니다.}\\ &:=& w - \alpha \cdot \dfrac{1}{2m} \dfrac{\delta}{\delta~w} \left( \displaystyle \sum_{i=1}^{m} \big( wx^{(i)} - y^{(i)} \big)^2 \right) & ~~~~~~~~~~ \text{미분하기 전에 상수를 밖으로 빼줍니다.}\\ &:=& w - \alpha \cdot \dfrac{1}{2m} \left( \displaystyle \sum_{i=1}^{m} 2 \big( wx^{(i)} - y^{(i)} \big) \cdot x^{(i)} \right) & ~~~~~~~~~~ \text{편미분 합니다.}\\ &:=& w - \alpha \cdot \dfrac{1}{m} \left( \displaystyle \sum_{i=1}^{m} \big( wx^{(i)} - y^{(i)} \big) \cdot x^{(i)} \right) & ~~~~~~~~~~ \text{도함수가 구해졌습니다.}\\ \end{eqnarray}$
(4)
이제 이 수식에 w와 learning rate를 대입하여 파라미터 w를 업데이트 합니다.
마찬가지로 계속해서 w와 learning rate만 대입해서 파라미터 w를 업데이트하면 모델을 최적화할 수 있을 것입니다.
참고.
편미분은 함수에 함수가 중첩된 경우의 미분방법을 말하며, 아래와 같이 미분합니다.
$f(g(x))' = f'(g(x)) \cdot g'(x)$
겉함수를 미분한 것과 속함수를 미분한 것을 곱하는 수식입니다.
Gradient Descent의 문제점과 해결¶
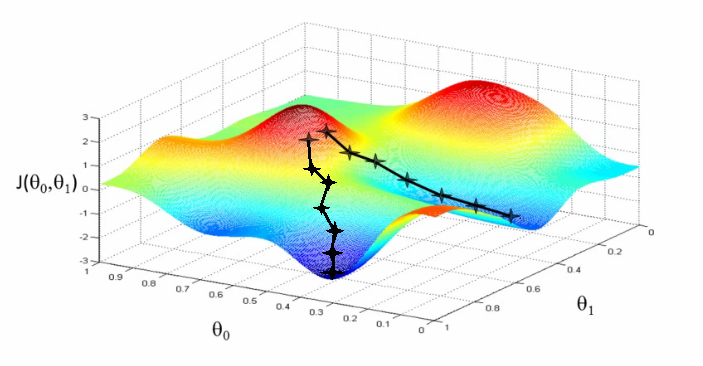
img src = www.holehouse.org/mlclass
(1) Initialization
Gradient Descent의 특징 중 하나는 위 그림과 같이 w를 어디서 시작하는가에 따라 종착지가 달라질 수 있습니다.
따라서 이를 해결하기 위해서 k번 각각 랜덤한 위치에서 시작하여 평균을 낸다던가 하는 방법을 사용할 수 있습니다.
import numpy as np
import matplotlib.pyplot as plt
x = np.linspace(1, 4, 101)
y = np.sin(x) + np.cos(5*x) + 1
plt.plot(x, y)
plt.plot([1.7, 2.1], [0.93,0.93], "orange")
plt.plot([3.0, 3.35], [-0.04,-0.04], "red")
plt.text(1.63, 0.7, "Local minimum")
plt.text(2.88, -0.25, "Global minimum")
plt.xlim(1.3, 3.7); plt.ylim(-0.5, 3)
plt.show()
(2) Local Minimum
또한 위의 그래프와 같이 Local minimum에 갖힐 수 있습니다.
이러한 Local minimum은 딥러닝의 Optimization 전반에서 중요한 문제중 하나인데
여러가지 기법들을 통해 이를 해결하고 있으며, 대표적으로는 기본적인 Vanilla SGD Optimizer보다 발전된 Optimizer를 사용하는 방법이 있습니다.
(Vanilla SGD는 여기에 소개된 것과 동일한 방법의 기본적인 Optimizer이며, 이후 Optimizer에 대한 종류를 다루면서 다시한번 설명합니다.)
'Basic fundamentals' 카테고리의 다른 글
| (5) Model Capacity (0) | 2020.01.13 |
|---|---|
| (4) What is Backpropagation? (0) | 2020.01.06 |
| (3) What is Neural Network? (0) | 2020.01.06 |
| (1) What is Loss Function? (0) | 2020.01.05 |
| (0) Overview of Fundamentals (0) | 2020.01.05 |
