| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | |
| 7 | 8 | 9 | 10 | 11 | 12 | 13 |
| 14 | 15 | 16 | 17 | 18 | 19 | 20 |
| 21 | 22 | 23 | 24 | 25 | 26 | 27 |
| 28 | 29 | 30 | 31 |
- version
- ResNet
- DCGAN
- jupyter
- Inception V1
- cnn
- GCN
- DL
- sigmoid
- vim-plug
- Bottleneck Layer
- Skip Connectioin
- Vanilla RNN
- iTerm2
- Manager
- python
- virtualenv
- GoogLeNet
- Inception Module
- classification
- Gated Skip Connection
- Residual Connection
- Regression
- Peephole Connection
- RNN
- Optimizer
- Generative
- Skip Connection
- Linear
- AI
- Today
- Total
IT Repository
(2) Basic of CNN - Convolutional Operation 본문
Convolutional Operation¶
Convolutional Layer를 소개하기 전에 이 레이어에 Convolution 이라는 이름이 붙게 된 이유인 Convolution 연산에 대해서 알아봅시다.
아래는 Convolution 연산을 설명하기 위한 사진입니다.
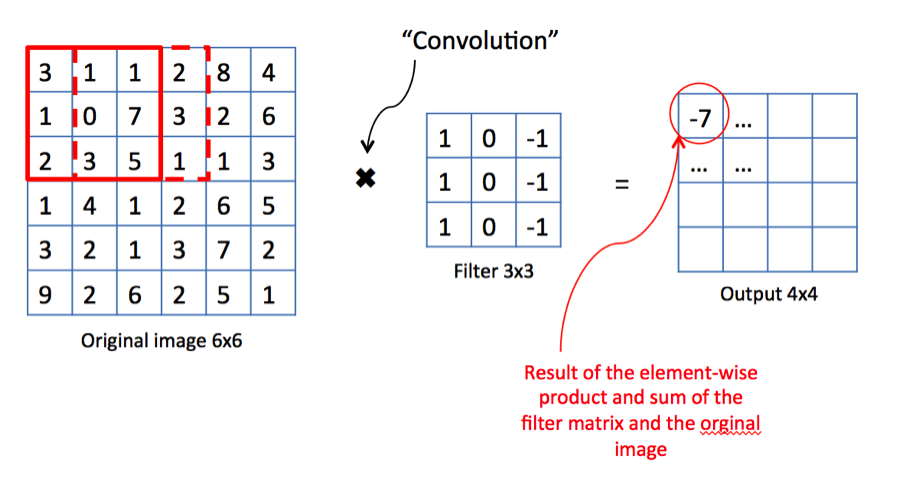
Convolution 연산은 기본적으로 어떠한 필터 행렬을 슬라이드 시키는 방식으로 작동합니다.
필터를 슬라이드 시켰을 때 겹치는 부분에 대해서 (1) Element-wise product를 하고, (2) 모두 더합니다.
참고.
Element-wise product: 행렬의 원소끼리 곱하는 것
Dot product: 일반적인 행렬간의 곱 연산
아래 코드 블럭은 위 사진의 빨간 박스 부분의 연산을 구현한 것으로써, 실제로 계산해보면서 이 부분을 이해하시기를 권합니다.
import numpy as np
elementwise_prod = np.array([[3,1,1], [1,0,7], [2,3,5]]) * np.array([[1,0,-1], [1,0,-1], [1,0,-1]]) # (1)
summation = np.sum(elementwise_prod) # (2)
Stride
위 사진과 같이 6x6 이미지에 3x3 필터를 1칸씩 이동시킨 Convolution 연산의 결과는 4x4 입니다.
그러면 이번에는 필터를 3칸씩 이동하면 결과가 어떻게 변할까요?
결과는 2x2가 되겠네요.
이와 같이 필터를 움직이는 간격을 Stride라고 합니다.
그리고 Stride를 변화시키면 아웃풋의 크기도 변한다는 것을 알 수 있습니다.
(zero)Padding
위의 사진을 다시한번 보면 Convolution 연산을 한번 거친 아웃풋은 크기가 줄어드는 것을 알 수 있습니다.
Convolution 연산을 거칠때마다 이미지의 크기가 줄면, 어쨌든간에 정보의 손실이 일어나게 됩니다.
그래서 이때 사용하는 것이 Padding 입니다.
Padding은 말 그대로 행렬의 주변을 어떤 값으로 한번 덧대는 것을 말하고, 일반적으로 0을 사용해서 Zero padding이라고 합니다.
그러면 6x6 행렬에 Padding을 한번해서 8x8 행렬로 만든 후에 필터를 이동시켜볼까요?
결과는 처음과 같은 크기인 6x6 행렬이 됩니다.
추가적으로는 Convolution 연산이 불가능할 때 Padding을 통해 연산을 가능하게 만들어주는 경우도 있고
아웃풋의 크기를 의도적으로 특정 크기로 맞추기 위해서 사용하는 경우도 있습니다.
(딥러닝에서 말하는 Convolution 연산은 수학이나 신호처리에서 사용하는 Convolution 연산과 조금 차이가 있습니다.)
Filtering with Conv Operation¶
이번에는 실제로 필터를 통해 디텍션이 되는 과정을 Convolutional 연산을 통해 알아봅시다.
아래에 7x7의 Grayscale 이미지가 있고, 3x3 필터를 통해 필터링 합니다.
import numpy as np
import matplotlib.pyplot as plt
Image = np.array([[0,0,1,1,1,0,0], [0,1,0,0,0,1,0], [1,0,0,0,0,0,1], [1,0,0,0,0,0,1]])
Image = np.concatenate([Image, Image[0:3][::-1]], axis=0)
diagonal_a = np.array([[0,0,1], [0,1,0], [1,0,0]])
diagonal_b = np.array([[1,0,0], [0,1,0], [0,0,1]])
vertical = np.array([[1,0,1], [1,0,1], [1,0,1]])
horizontal = np.array([[1,1,1], [0,0,0], [1,1,1]])
def imshow(ax, array2d, title=None):
if title:
ax.set_title(title)
ax.axis("off")
ax.imshow(array2d, cmap="gray", vmin=0, vmax=1.1)
height, width = array2d.shape
for h in range(height):
for w in range(width):
value = array2d[h, w]
ax.text(w, h, value, c="white" if value==0 else "black")
plt.figure(figsize=(20, 10))
ax1 = plt.subplot(2,4,1); imshow(ax1, Image, "Original Image")
ax1.add_patch(plt.Rectangle((-0.5,-0.5), 3, 3, fill=False, linewidth=3, color="red"))
ax1.add_patch(plt.Rectangle((3.5,-0.5), 3, 3, fill=False, linewidth=3, color="green"))
ax1.add_patch(plt.Rectangle((1.5,3.5), 3, 3, fill=False, linewidth=3, color="blue"))
ax2 = plt.subplot(2,4,5); imshow(ax2, diagonal_a, "Filter A")
ax3 = plt.subplot(2,4,6); imshow(ax3, diagonal_b, "Filter B")
ax4 = plt.subplot(2,4,7); imshow(ax4, vertical, "Filter C")
ax5 = plt.subplot(2,4,8); imshow(ax5, horizontal, "Filter D")
plt.show()
(1)
원본이미지의 RED 구역에 A필터를 씌워서 Conv 연산을 하면 결과는 3입니다.
나머지 구역에 A필터를 씌워도 결과는 1밖에 나오지 않습니다.
즉, A필터는 오른쪽에서 왼쪽으로 내려오는 대각선을 검출하는 필터입니다.
(2)
반대로 B필터는 GREEN 구역에서만 3이고 나머지 구역에서는 1입니다.
B필터는 왼쪽에서 오른쪽으로 내려오는 대각선을 검출하는 필터입니다.
(3)
마지막으로 C와 D는 각각 세로와 가로에서 3, 나머지에서는 2의 결과를 가집니다.
C는 세로를 검출하는 필터, D는 가로를 검출하는 필터입니다.
물론 아래와 같이 필터를 만들면 각각 3과 1의 결과만 낼 테니 더욱 명확하게 필터링이 가능해지겠죠.
plt.figure(figsize=(20, 5))
ax1 = plt.subplot(1,4,1); imshow(ax1, np.array([[1,0,0],[1,0,0],[1,0,0]]), "Filter C-1")
ax2 = plt.subplot(1,4,2); imshow(ax2, np.array([[0,0,1],[0,0,1],[0,0,1]]), "Filter C-2")
ax3 = plt.subplot(1,4,3); imshow(ax3, np.array([[1,1,1],[0,0,0],[0,0,0]]), "Filter D-1")
ax4 = plt.subplot(1,4,4); imshow(ax4, np.array([[0,0,0],[0,0,0],[1,1,1]]), "Filter D-2")
plt.show()
중요한 것은 이러한 필터들의 디텍션 결과를 합치면 원본 이미지의 형상을 알아낼 수가 있을거 라는 것입니다.
여기서는 단순한 Grayscale 정팔각형으로 각각 엣지만 검출하면 충분히 어떠한 도형인지 알아내는 것이 가능했지만,
실제로는 이렇게 엣지를 검출해서 다음 층에 전달하고 다음 층에서는 조금더 복잡한 형태의 엣지나 질감 등을 검출해내는 방식으로 Convolution 연산이 작동하게 됩니다.
(여기서는 Grayscale을 사용했지만, RGB라면 가로세로는 동일하지만 깊이가 3인 필터를 통해서 동일한 방식으로 필터링이 가능합니다.)
즉, 여러개의 필터로 Convolution 연산을 해서 파악한 특징을 추출하는 것이 Convolution Layer의 역할입니다.
'CNN > Study' 카테고리의 다른 글
| (5) VGGNet (Small Filters with Deeper Networks) (0) | 2020.01.14 |
|---|---|
| (4) AlexNet (0) | 2020.01.14 |
| (3) Basic of CNN - Structure of CNN (4) | 2020.01.14 |
| (1) Basic of CNN - What is CNN (0) | 2020.01.14 |
| (0) Overview of CNN (0) | 2020.01.14 |
