| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- DCGAN
- python
- Inception V1
- vim-plug
- Residual Connection
- Peephole Connection
- classification
- Regression
- Vanilla RNN
- jupyter
- GCN
- Skip Connection
- Optimizer
- iTerm2
- virtualenv
- GoogLeNet
- Generative
- RNN
- Linear
- Manager
- cnn
- sigmoid
- Inception Module
- AI
- DL
- version
- Bottleneck Layer
- Gated Skip Connection
- Skip Connectioin
- ResNet
- Today
- Total
IT Repository
(3) Basic of CNN - Structure of CNN 본문
Convolutional Layer¶
이제 Convolution Layer를 알아보면서 기존의 FC Layer와 어떤 점이 다른지를 확인해보려고 합니다.
(1)
이미 설명했듯이 FC 레이어는 이미지를 다루기 위해서 이미지 행렬을 한 줄로 쭉 펴는 작업(Flatten)이 필요합니다.
이렇게 되면 이미지에서는 분명히 붙어있는 픽셀인데 Flatten한 행렬에서는 서로 떨어져버립니다.
즉, 이미지의 공간적인 구조(Spatial structure)가 무시되어 버립니다.
(2)
반면에 이를 Convolutional 레이어는 Convolutional 연산을 사용합니다.
따라서 필터를 슬라이드함으로써 주위 픽셀들을 계산하면서 이미지의 공간적인 구조를 보존하게 됩니다.
Conv 연산을 하면 필터의 크기와, Stride, Padding 유/무 를 통해서 아웃풋의 크기가 고정됩니다.
그러면 아웃풋의 차원은 무엇으로 결정할까요?
필터의 개수가 아웃풋의 차원을 결정하게 됩니다. (이전에 했던 여러가지 필터를 사용해서 필터링을 하는 것과 동일합니다.)
이를 통해 CNN 모델의 너비를 늘릴 수도 줄일 수도 있습니다.
아래는 Conv 레이어의 각 파라미터에 대한 수학적 계산식입니다.
조금 생각하면 크게 어렵지 않은 수식일 것입니다.
- Accepts a volume of size $D_1 \times W_1 \times H_1$
- Requires 4 hyperparameters:
- Number of filters $K$
- Size of filters $F$
- the stride $S$
- the amount of zero padding $P$
- Produces a volume of size $D_2 \times W_2 \times H_2$
- $W_2 = (W_1 - F + 2P)~/~S + 1$
- $H_2 = (H_1 - F + 2P)~/~S + 1$
- $D_2 = K$
Receptive Field¶

각 필터들이 배출한 하나의 결과값은 하나의 뉴런입니다.
하나의 뉴런이 원본 이미지에서 담당하는 범위를 Receptive field라고 합니다.
위 사진의 초록색 뉴런의 Receptive Field는 원본 이미지의 3x3 부분이고
노란색 뉴런은 원본이미지의 5x5 부분입니다.
즉, 층이 깊어질 수록 더 넓은 Receptive field를 가지게 됩니다.
Pooling Layer¶
1600x900 크기의 고해상도 이미지에서 사람 얼굴에 있는 살색 픽셀 하나의 값은 의미가 적거나 거의 없습니다.
만약, 이미지의 크기를 다운샘플링한다면 하나의 값이 더 함축적인 의미를 가지게 될 것이고 함축적인 정보는 모델의 성능에 있어 효율적이고 효과적입니다.
이와 같이 이미지가 갖는 정보를 함축적으로 만들기 위해 Pooling Layer를 사용합니다.
Pooling의 방법에는 여러가지가 있는데 대표적인 방법으로는
- Max Pooling
- Average Pooling
이 있습니다.
(1)
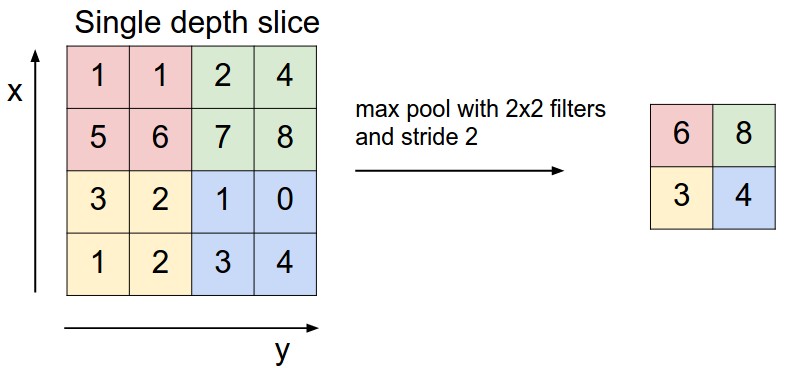
위 그림은 Max Pooling을 설명하고 있습니다.
2x2 필터를 댄 구역에서 가장 크게 Activate된 뉴런의 정보를 사용하는 것이 Max Pooling 입니다.
(2)
Average Pooling은 필터를 댄 구역의 값들의 평균을 사용하는 것입니다.
그러나 Pooling을 거친 후에 정보의 강도가 약해지는 이유로 인해 잘 사용하지 않습니다.
일반적으로 2x2 필터(커널) 사이즈로 Stride=2를 주고 사용합니다.
이렇게 하는 경우에 Pooling Layer의 아웃풋이 1/2이 되는 특징이 있습니다.
(만약 3x3, stride=3 이라면 1/3이 되겠죠.)
Structure of CNN¶
Conv Net은 아래의 레이어를 반복해서 거치면서 최초 이미지의 Sparse한 정보를 Dense한 정보로 변환합니다.
- Convolutional Layer
- Activation Function (앞서 Activation을 하지 않으면 Non-linearity를 확보할 수 없다는 것을 배웠습니다.)
- Pooling Layer (반드시 들어가는 것은 아니지만, 기본 구조로써 사용합니다.)
예를 들면 아래와 같습니다.
- Input = (3, 256, 256)
- Convolutional Layer (filters=64, filter_size=3x3, stride=1, padding=True) ⇒ (64, 256, 256)
- Activation Function
- Pooling Layer (kernel_size=2x2, stride=2) ⇒ (64, 128, 128)
Classifier¶
Conv Net을 거치면 중요한 정보가 Feature map에 포함됩니다.
결국, 원본 이미지의 Sparse한 정보를 Dense한 정보로 만드는 것이 Conv Layer의 역할이고 그 밀집된 정보를 통해 앞서 해왔던 문제들과 동일하게 FC Layer를 사용해서 분류 합니다.
Binary Class라면 Sigmoid를 사용하면 될 것이고, Multinomial Class라면 Softmax를 사용하면 될 것입니다.
(물론 Convolution 연산을 거친 아웃풋 텐서는 3차원의 데이터이므로 FC Layer로 다루기 위해서 Flatten을 해주어야 합니다.)
주로 이미지를 통해 하는 것이 분류 문제가 많기 때문에 분류 문제를 예시로 들었지만
다른 문제에 적용하기 위해서도 마찬가지로 Convolution 연산을 통해서 고차원의 정보를 추출한다는 관점으로 접근하면 동일할 것입니다.
Variations of CNN¶
CNN 아키텍쳐는 단순하게 CNN으로 사용되기도 하지만 RNN과 결합한 구조로도 사용됩니다.
그 예로는 RCNN이나 Convolutional RNN 이 있습니다.
(이에 관해서는 추후에 포스팅 하겠습니다.)
또한, 일반적으로 이미지를 다루기 위해 사용하는 Conv 2d 대신에 Conv 1d를 사용해서 RNN의 전유물이었던 텍스트 시퀀스 데이터를 다룰 수도 있습니다.
Conv 1d를 사용한 텍스트 모델은 일반적으로 RNN보다 빠른 속도를 보입니다.
(이 역시 추후에 포스팅 하겠습니다.)
'CNN > Study' 카테고리의 다른 글
| (5) VGGNet (Small Filters with Deeper Networks) (0) | 2020.01.14 |
|---|---|
| (4) AlexNet (0) | 2020.01.14 |
| (2) Basic of CNN - Convolutional Operation (0) | 2020.01.14 |
| (1) Basic of CNN - What is CNN (0) | 2020.01.14 |
| (0) Overview of CNN (0) | 2020.01.14 |
